《学习JavaScript数据结构与算法》笔记---树

本文源码 这里

什么是树

1.一种非线性结构,由n(n>=1)个有限节点组成的有层次关系的集合
2.如下图：

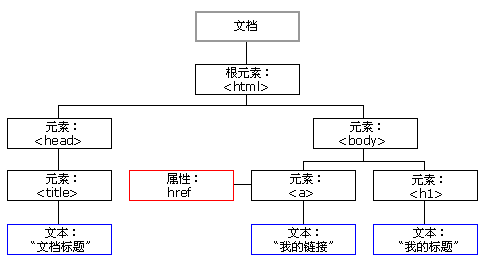
3.HTML的所有dom节点其实就是一棵dom树，如图

树的特点

优点

• 1.因为基于链表实现，所以集成了链表的优点；但又因为非线性结构的原因查询比链表有效率；
• 2.虽然查询效率不集哈希表，但比哈希表节省空间；
• 3.也改善了数组插入和删除时，效率低下的原因；
• 4.可以表示一对多的关系；

缺点

• 1.查找删除效率取决该树的深度，深度越大效率越低
• 2.查找效率没有哈希表更有效率

---

存在即合理，根据自己会继续要选择合适的结构

---

关于树的一些术语

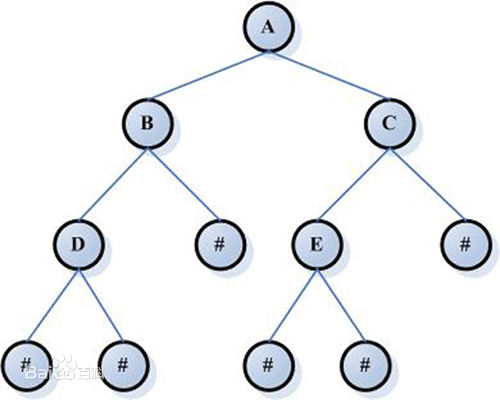
1.位于顶部的节点叫做根节点；图中的A
2.树中的每个元素叫做节点；图中的所有圆点
3.内部节点：有子节点的节点；图中的abcde
4.外部节点也叫叶节点：没有子节点的节点；图中的#
5.父节点：a时bc的父节点；是其他节点的祖先节点；
6.子节点：bc是a的子节点；
7.子树：由某个子节点和他的子节点组成的树；
8.节点的度:节点的子节点个数
9.节点的层：根节点是1层(或0层),子节点层数依次加一；
10.树的深度：层数最大的节点；是树的深度

一些常见树

二叉树(Binary Tree)

• 1.每个节点的子节点个数最多只有2个；一个左节点，一个右节点
• 2.二叉树i层的最大节点树为 2的i-1次方,i>=1;
• 3.深度为k的二叉树的最大节点总数为 2的k次方后再-1；k>=1
• 4.非空二叉树的叶结点个数n0=n2+1； n2为叶节点个数

完美二叉树

• 除过根节点其他所有子节点都有2个子节点的二叉树

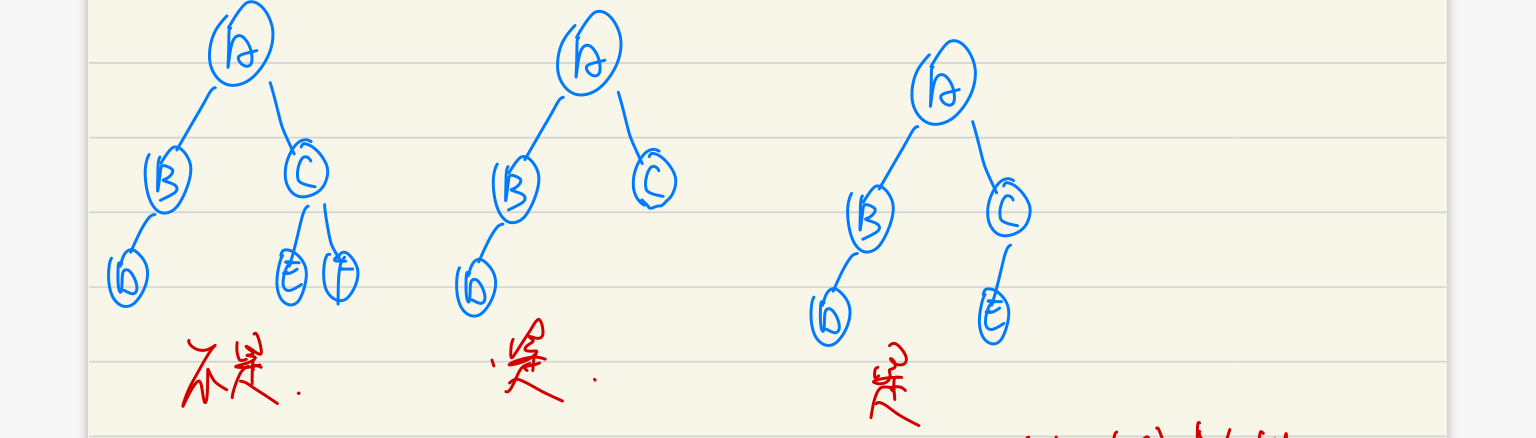
完全二叉树(Complete Binary Tree)

• 1.除过根节点其他所有子节点都有2个子节点；
• 2.且最后一层从左到右叶节点连续存在，只缺右边若干接点的二叉树
• 3.完美二叉树时特殊的完全二叉树
• 4.举例子
  

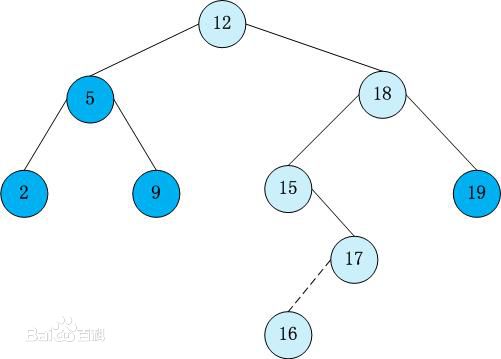
二叉搜索树(Binary Search Tree) 重点

• 非空*左**子树的所有值小于***其根节点；
• 非空*右**子树的所有值大于***其根节点；
• 每一个子树也都满足二叉搜索树规则；
  ;

非平衡树

1.一颗左右子树节点分布不平衡的树，叫做非平衡树
2.一颗非平衡树相当于写了一个链表，体现不出树的优势；
;

平衡树

1.也是二叉搜索树
2.每个节点的左子树节点个数和右子树节点个数相近
3.在二叉搜索树的实现上多封装了一些条件来保证不会出现非平衡树那样的情况的树
常见平衡树:

• AVL树:不常用
• 红黑树