《学习JavaScript数据结构与算法》笔记---图论
本文源码 这里
什么是图
1.图是网络结构的抽象模型
2.由一组边连接的顶点(或节点)组成
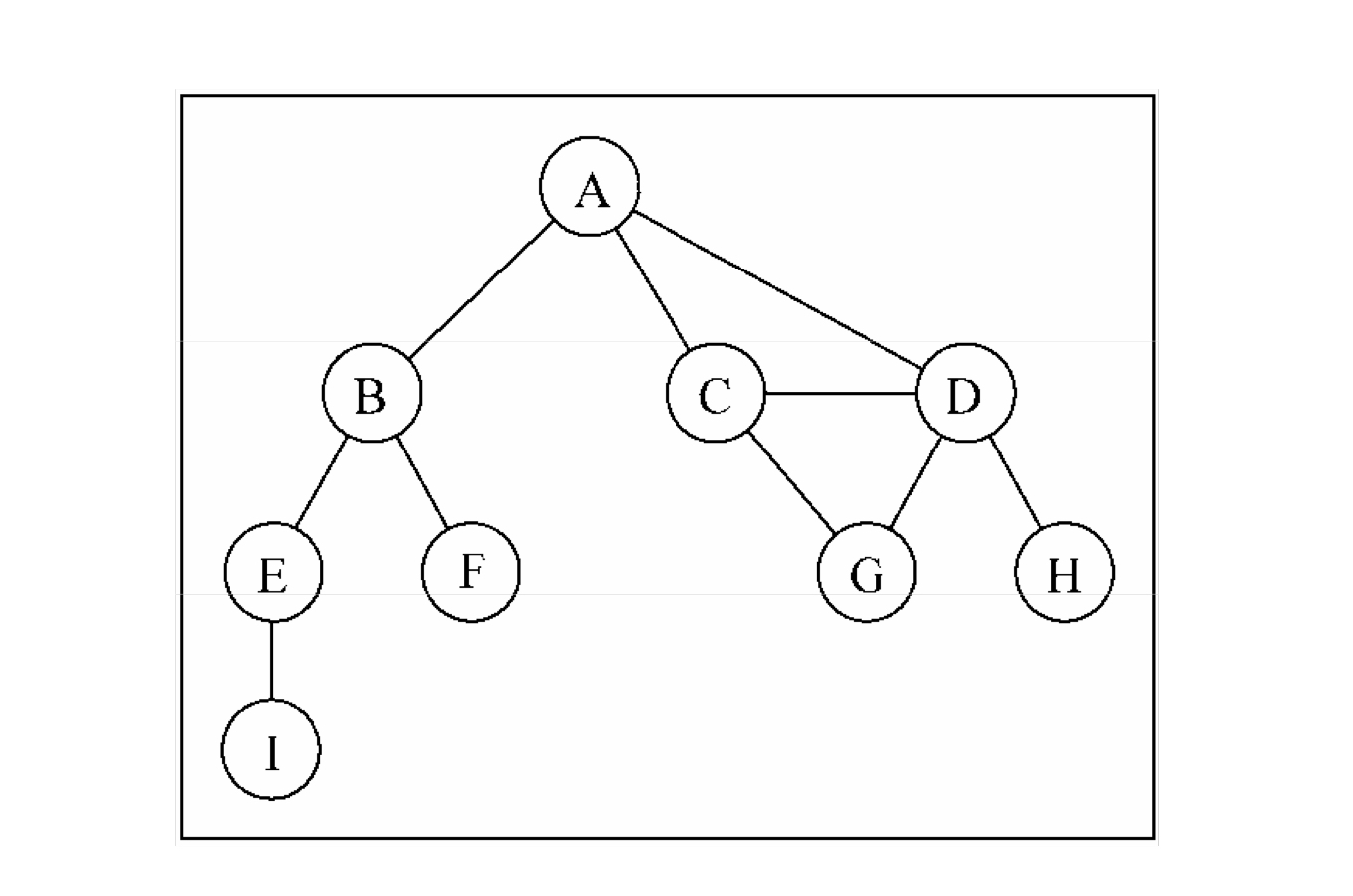
图和树的区别
1.树和链表也是图的一种
2.但是和树不同,树的左右两个子树的节点不可以相连,图可以(如上图)
图可以干嘛
用来抽象实际生活中某些关系网的结构,比如
- 1.人际关系网抽象成图,每个人就是这张图中的点,人与人之间的关系就是点点之间的连线
- 2.地铁站点图,每个站就是一个顶点,站与站之间的路线就是一条边
关于图的术语
顶点:图中的一个点;比如在地铁图中的某一站;人际关系网中某个人
边:顶点之间的距离;比如地铁图中两站之间的距离
相邻顶点:一条边链接在一起的2个顶点称为相邻顶点
度:一个顶点的度是相邻顶点的数量
出度:某个顶点指向别的顶点的数量
入度:别的顶点指向某个顶点的数量
路径:两顶点之间经过的所有顶点构成的一个顶点序列称为路径,可以有多个;
- 简单路径:顶点序列中不包含重复的顶点
- 回路:顶点序列的第一项和最后一项是同一个顶点;就是从一个顶点出发转一圈又回到该点
无向图:假设有AB两个顶点通过一条边连接在一起,可以从A-B也可以从B-A,这条边没有方向,就称为无向图;(如上图)
有向图:假设有AB两个顶点通过一条边连接在一起,只可以从A->B或B->A,称为有向图(下图)
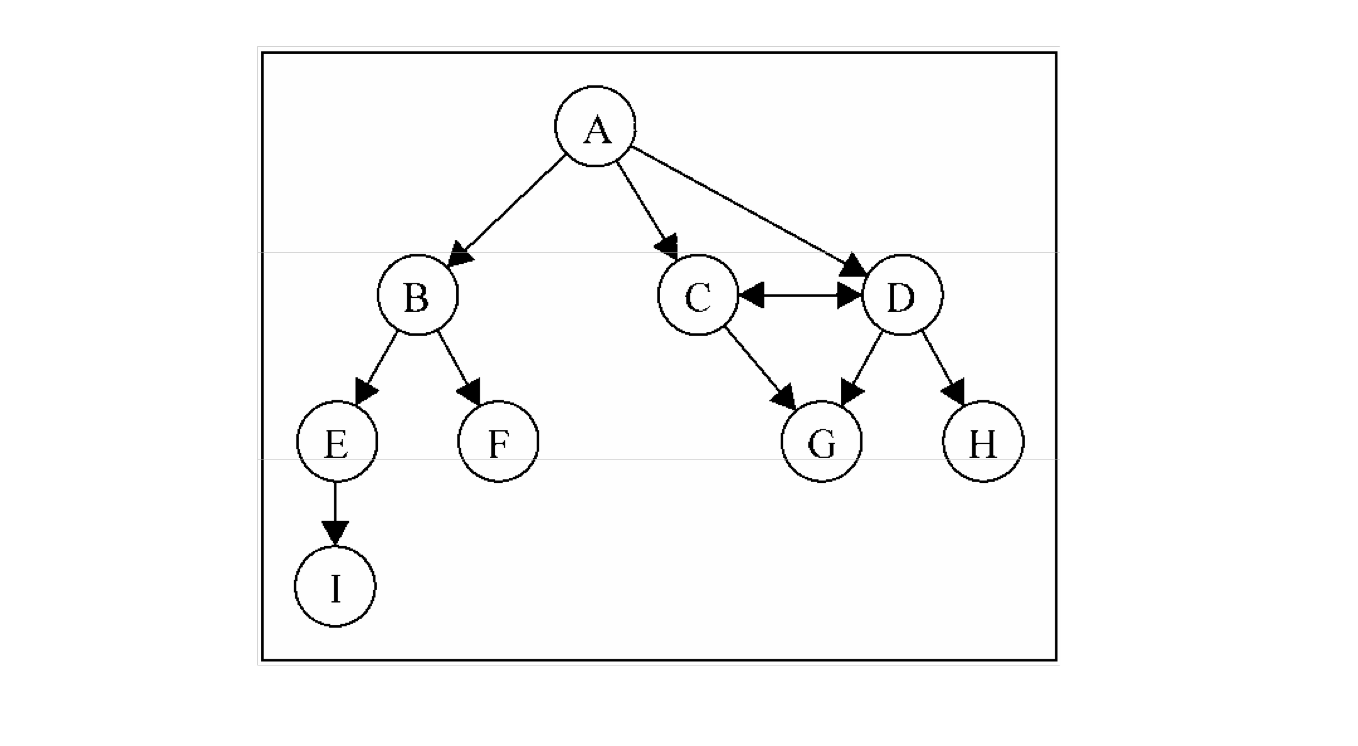
无权图:图中的边没有携带权重,称为无权图(上面两个图都是)
带权图:边有一定的权重;这个权重可以表示各种想表示的数据,比如花费时间,顺序,等等
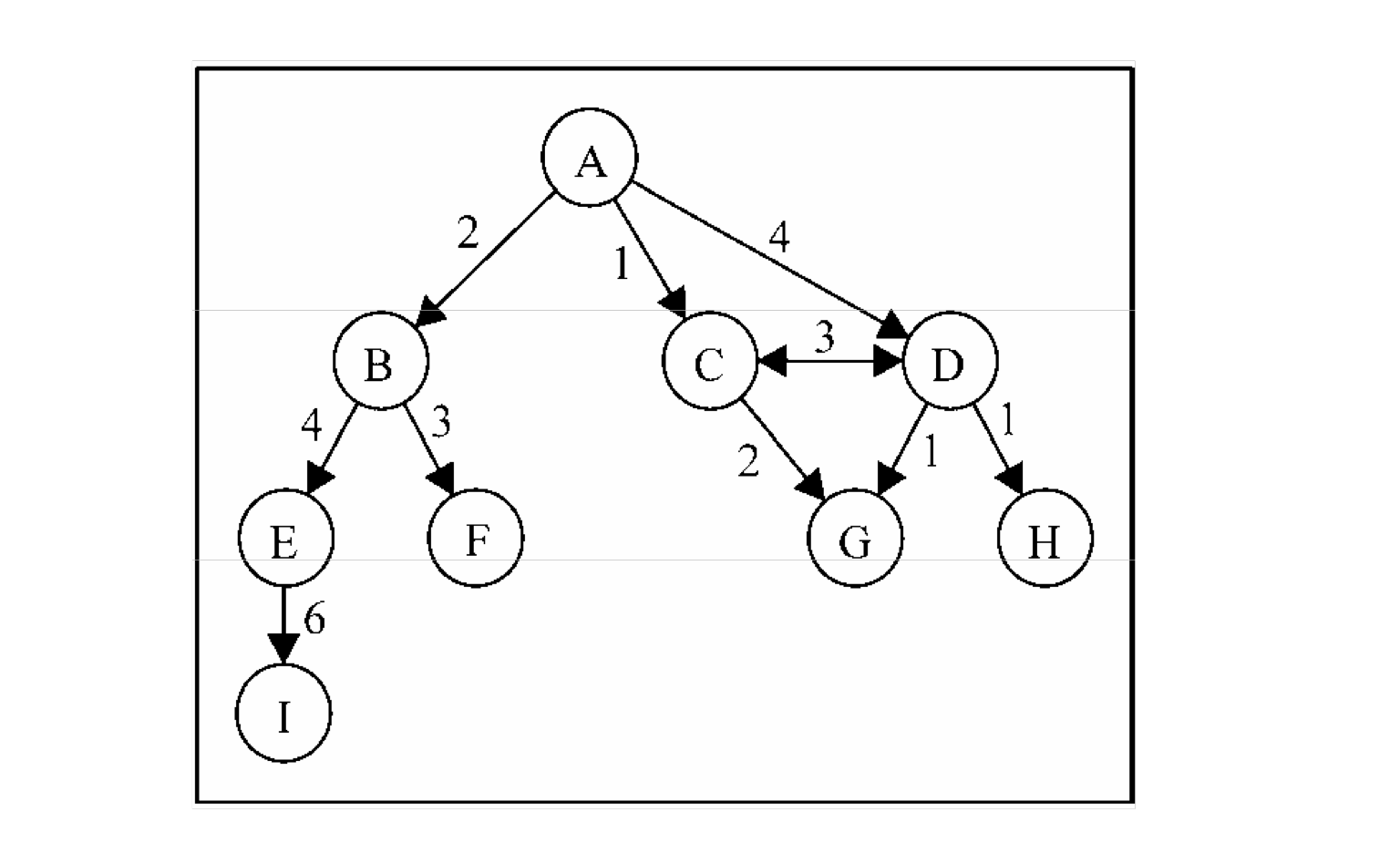
用代码表示图
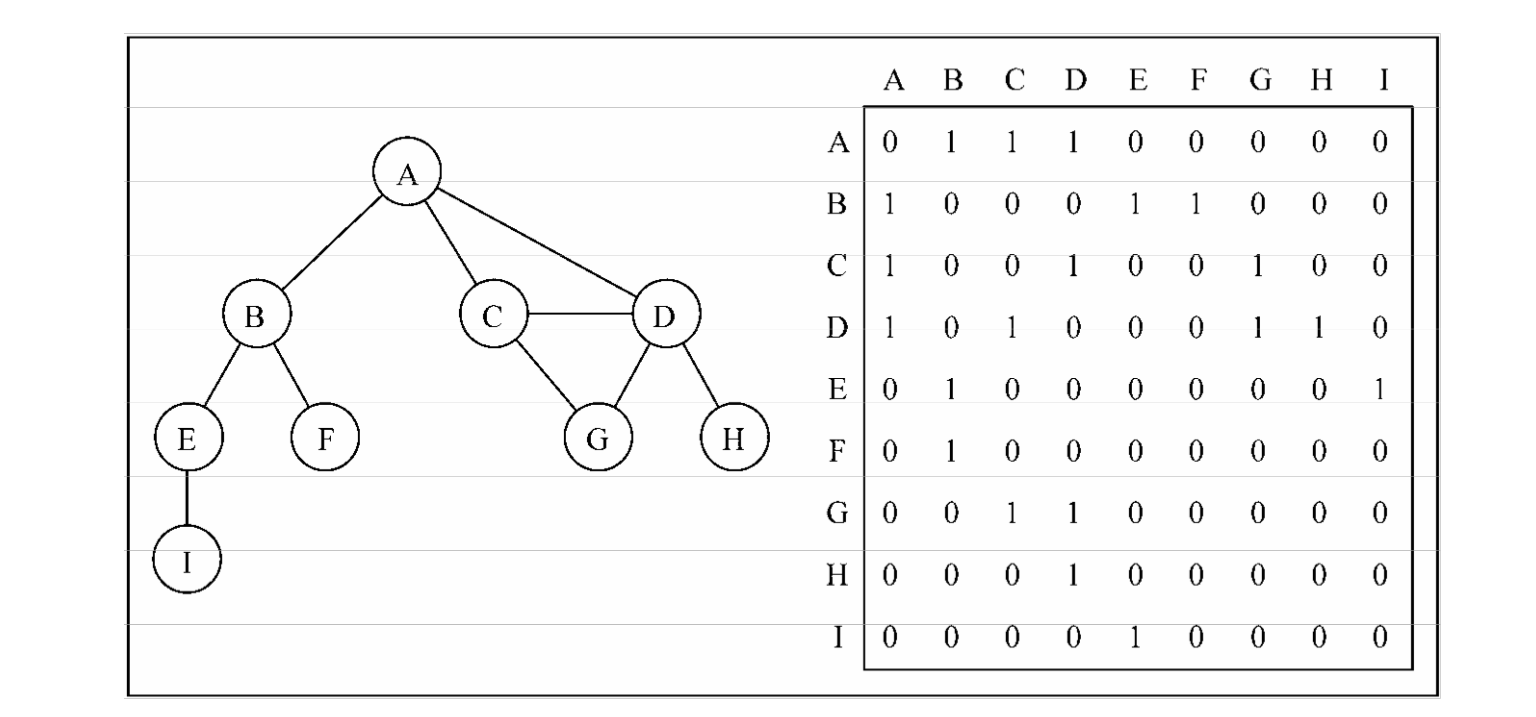
使用邻接矩阵(表示顶点之间相邻关系的矩阵)
- 1.用数字或者字母表示顶点,然后用一维数组存放顶点(和顶点包含的数据)
- 2.用一个二维数组表示顶点之间的链接(边);
- 2.1假设a-b相连,即表示1,不相连表示0;
- 2.2顶点到自己本身没有边,成为自回路,也用0表示
- 2.3如果边带权重,当两点相连时,可以把这个数字按一定规则来表示
- 2.4邻接矩阵表示无向图时,一定是对称的
- 3.邻接矩阵的问题:
- 3.1表示稀疏图(顶点之间的边很少的图)的时候会浪费很多内存空间,因为用0表示了很多不存在的边
- 4.多用于表示无向图
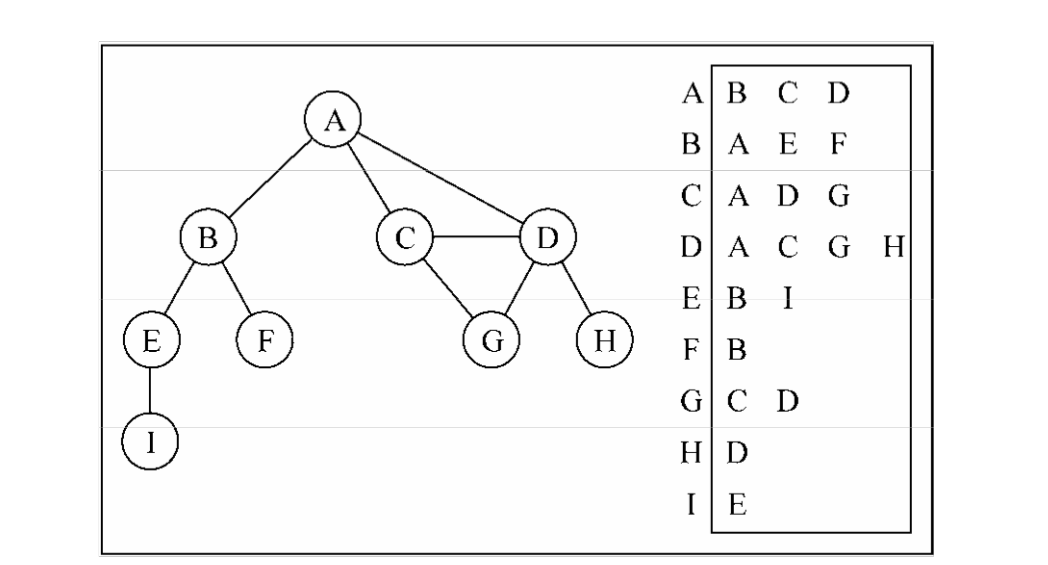
使用邻接表(本文也是用这种方式)
- 1.邻接表由顶点和相邻顶点的顶点列表组成
- 2.数组/链表/字典(哈希表)都可以实现
- 3.多用于表示有向图
- 4.邻接表的问题
- 4.1计算出度比较简单
- 4.2计算入度非常麻烦
关于图的遍历
1.需要注意的时,遍历时不能重复访问某个节点,且需要指定第一个要访问的节点,一般对图的遍历常用的有一下2种算法
2.广度优先算法(BFS)
- 特点:优先遍历当前访问节点的相邻节点 ,属于一层一层遍历
- 使用队列实现
3.深度优先算法(DFS)
- 特点:有点类似树的先序遍历,沿着路径,一条路径的节点全部访问完毕后,再返回有分支路径的节点去访问另一条路径;
- 可以使用栈,或者递归(本文使用递归)来实现
4.上述的两种方式遍历结果的区别:如图
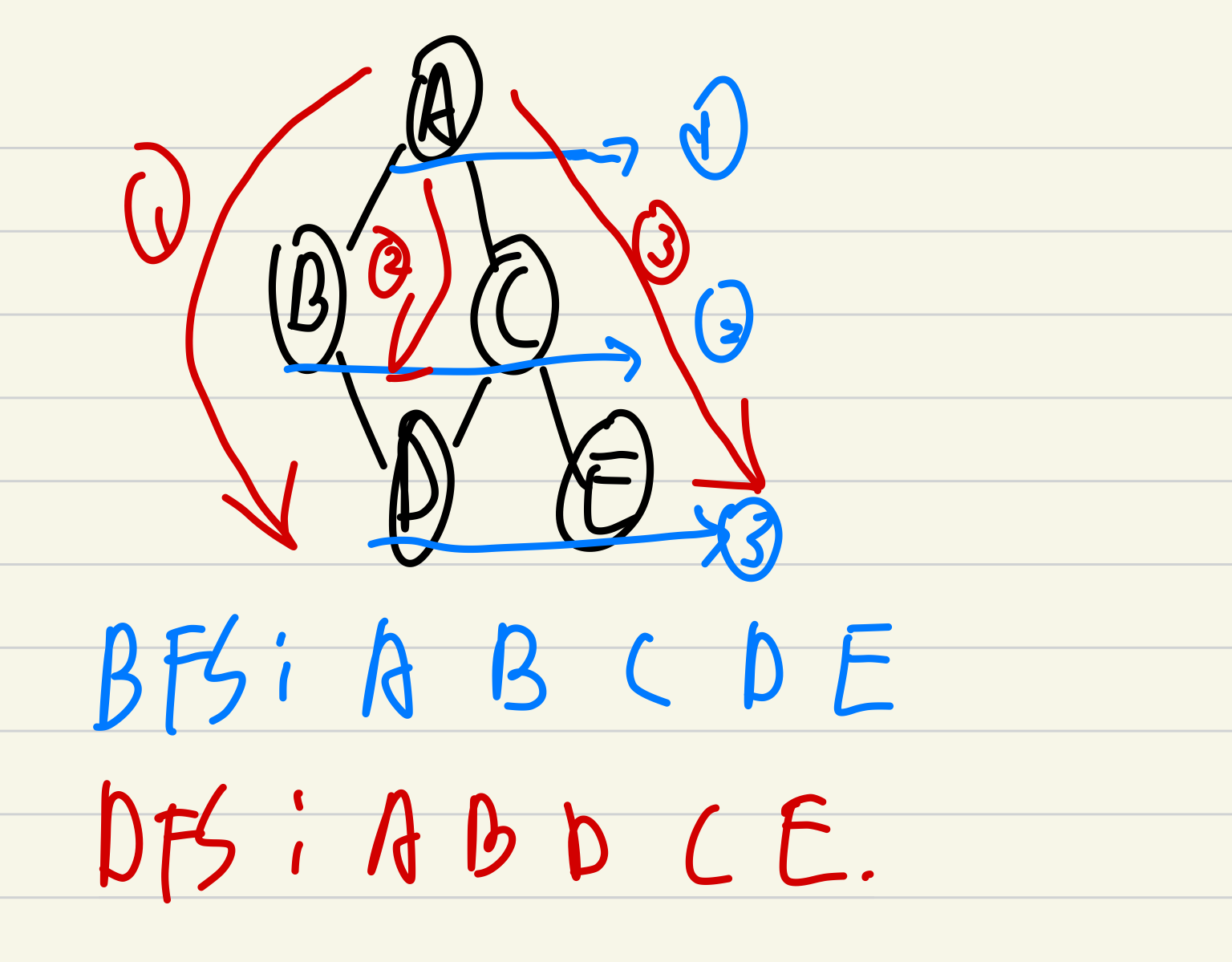
表示节点的状态
白色:表示顶点还没有被访问
灰色:表示该顶点被访问过,但未被探索过(就是和他连接的点还未被访问)
黑色:表示该顶点被访问过且被完全探索过(该点和该点相连的顶点都被访问过)
遍历算法
开始前先做一点说明
- 1.我们用一个数组存储所有的顶点
- 2.然后用一个对象存储相连点的关系:key为一个点,value是一个数组,存储和该点相连的点
1
2
3
4function Graph() {
this.vertexes = [];
this.eage = {};
}
BFS
实现思路:
- 1.每次访问一个节点时,把和它相连的节点插入队列
- 2.一个节点访问完毕后,在读取队列中先进队列的节点开始访问,
- 3.然后重复执行12,直到队列为空,结束
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37// 参数:指定第一个访问节点 callback
Graph.prototype.BFS = function (initV, handler) {
if (this.check(initV)) {
// 1.初始化颜色
let color = this.initColor();
// 2.创建队列
let que = new Queue();
// 3.将第一个顶点插入队列
que.enqueue(initV);
// 4.循环队列取出元素
while (!que.isEmpty()) {
// 4.1取出顶点
let v = que.dequeue();
// 4.2获取顶点的相邻顶点
let vList = this.eage[v];
// 4.3将v颜色设置成灰色
color[v] = 'gray';
// 4.4把相邻顶点插入队列
for (let i = 0; i < vList.length; i++) {
// 遍历相邻节点
let e = vList[i];
// 检查该点之前有没有被访问过
if (color[e] == 'white') {
console.log(e);
color[e] = 'gray';
que.enqueue(e);
}
}
// 4.5.访问v节点
handler(v);
// 4.6访问完毕
color[v] = 'black';
}
} else {
console.error('检查顶点是否存在');
}
};
DFS
实现思路:
- 通过递归函数,访问一个节点的相邻节点
1 | |
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!